音がなる仕組み(矩形波オシレータ)
矩形波オシレータの音がなる仕組みについて考えていきたいと思います。
簡単なイメージ
図のように、この回路は発振部分と音量調節部分に分かれています。
発振部分
コンデンサに電気がたまったり抜けたりを繰り返しています。ししおどしのように、コンデンサに電気がたまると抜けていき、抜けていくとまたたまりだすというイメージです。
コンデンサに電気が貯まるとNOT回路の入力電圧が大きくなるのでやがてしきい値電圧を超え、出力はLOWになります。するとコンデンサの電気が抜けていって今度は入力電圧がしきい値を下回り、出力はHIGHになります。そうすると今度はコンデンサに電気が再びたまっていきます。
これを繰り返していくことにより、NOT回路の出力はHIGH, LOW, HIGH, LOW, …と続いていき、矩形波ができることになります。
音量調節部分
可変抵抗で電圧を分圧することによって音量を調節しています。
バッファ
あとに続く回路はボルテージフォロワ回路で、バッファのために入れています。
音の波形のでき方
発振部分ではどのようにして音の波形ができているのか、式も使いながら考えていきます。微分方程式を使っていくので多少難しいかもしれません。
コンデンサに電気がたまる・抜ける様子

図のような回路を考え、コンデンサの電荷の様子を計算で求めてみます。
コンデンサにたまった電荷を\(Q\)とします。
微分方程式は以下のようになります。
$$V_{out} = R\frac{dQ}{dt} + \frac{Q}{C}$$
これを\(Q\)について解くと次のようになります(\(A\)は定数)。
$$Q(t) = A e^{-\frac{1}{RC}t} + CV_{out}$$
VoutがHIGHのとき(電気がたまる)
$$V_{out} = V_H$$
と表すことにします。
初期値が
$$Q(0) = 0$$
であったとすると、電荷\(Q\)の式は以下のようになり、下のグラフになります。これが、コンデンサに電気がたまっていく様子です。
$$Q = CV_{H} ( 1 – e^{-\frac{1}{RC}t })$$

VoutがLOWのとき(電気が抜ける)
$$V_{out} = 0$$
と表すことにします。
今度は初期値が
$$Q(0) = CV_H$$
であったとすると、電荷\(Q\)の式は以下のようになり、下のグラフになります。これが、コンデンサから電気が抜けていく様子です。
$$Q = CV_{H} e^{-\frac{1}{RC}t}$$

NOT回路の動く様子
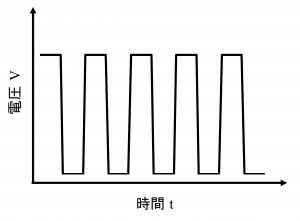
NOT回路とは、入力にHIGHが来るとLOWを出力し、入力にLOWが来るとHIGHを出力する回路です。出力の変わる境目の電圧をしきい値電圧といいます。
回路の動きを考えるにあたって、NOT回路のしきい値電圧を考える必要があります。
今回使用しているSN54HC14というNOT回路はシュミットトリガインバータです。
シュミットトリガというのは、簡単に言うと、しきい値が2つあるということです。
図のように、出力電圧が下から上に行くときのしきい値\(V_{LH}\)と、上から下に行くときのしきい値\(V_{HL}\)の2つがあります。
オシレータの発振部分
最後に、上の2つの節で考えた回路を組み合わせたものを考えていきます。

この回路はオシレータの発振部分とほとんど同じです。違う部分は、複数の抵抗と可変抵抗が1つの抵抗で表現されていることと、NOT回路が1つしかないことですが、回路の動きとしては同じだと考えて大丈夫です。
上の節で考えた回路2つが合わさっているので複雑に感じるかもしれませんが、実際はそんなことないです。なぜなら、NOT回路に流れる電流は非常に小さく、無視できるからです。つまり、上で考えたことがそのまま適用できます。
VoutがHIGH(電気がたまる)とき
初め\(V_{out}\)がHIGHだとすると、コンデンサには電気が溜まっていきます。ただし今回は上の節と異なり、NOT回路がつながっています。すると、上で考えたようにコンデンサの電圧\(V_{cap}\)が\(V_H\)になるまで電気がたまるということは起こりません。なぜなら、NOT回路は入力がしきい値電圧\(V_{HL}\)を超えると出力\(V_{out}\)がLOWに変化するからです。
下図のように、コンデンサには赤い部分までしか電気がたまらないことになります。
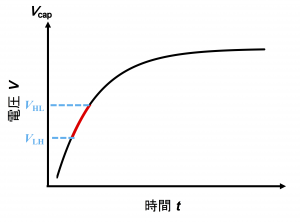
VoutがLOW(電気が抜ける)とき
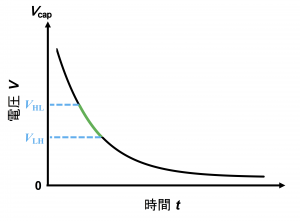
コンデンサの電圧\(V_{cap}\)が\(V_{HL}\)に達すると、NOT回路はLOWを出力するので今度はコンデンサから電気が抜けていきます。ただし、ここでもNOT回路がつながっていることで0 Vまで電気は抜けていきません。
コンデンサの電圧\(V_{cap}\)がNOT回路のしきい値電圧\(V_{LH}\)を下回ると、今度はNOT回路の出力\(V_{out}\)がHIGHに変わります。
なので、下図のようにコンデンサからは緑の部分までしか電気が抜けません。
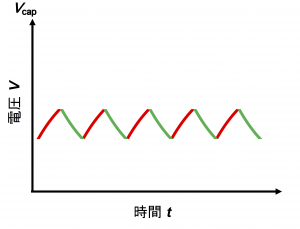
電気がたまる、抜けるを繰り返す
回路をずっと動かしていると、\(V_{LH} \leq V_{cap} \leq V_{HL}\)の範囲でコンデンサに電気がたまったり抜けたりを繰り返すことになります。つまり、赤と緑の部分を繰り返し、下図のようになり、三角波ができます。ここまでは三角波オシレータのなる仕組みと同じです。
ここまでは\(V_{cap}\)に注目していましたが、今度は\(V_{out}\)に注目していきます。\(V_{out}\)はグラフの赤い部分でHIGH、緑の部分でLOWとなるので、グラフは下図のようになり、矩形波ができます。
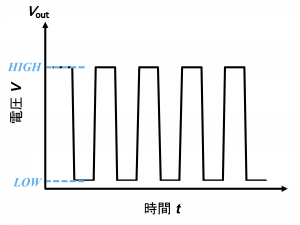
(もし間違いに気づい方がいらっしゃいましたらコメントにて連絡していただけると幸いです。)